Optimal number of clusters

Learn how to easily evaluate clustering algorithms and determine the optimal number of clusters using the below methods:

• Elbow curve plots the sum of squared errors (squared errors summed across all points) for each value of k.

• Silhouette analysis determines if individual points are correctly assigned to their clusters.

import matplotlib
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn_evaluation import plot

matplotlib.rcParams["figure.figsize"] = (7, 7)
matplotlib.rcParams["font.size"] = 18

# get data for clustering
X, y = datasets.make_blobs(
    n_samples=500,
    n_features=2,
    centers=4,
    cluster_std=1,
    center_box=(-10.0, 10.0),
    shuffle=True,
    random_state=1,
)

# Fit kMeans on the data
kmeans = KMeans(random_state=10, n_init=5)

Elbow curve

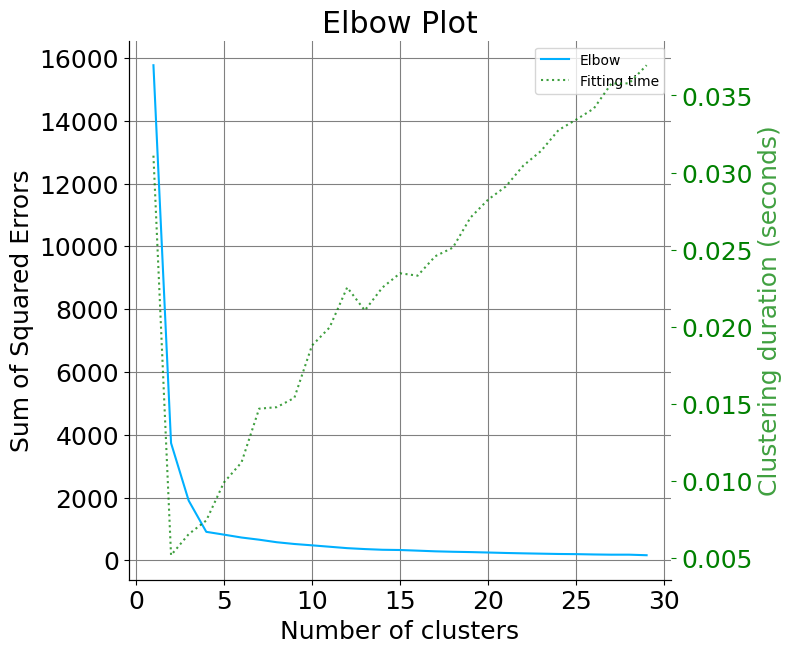
Elbow curve helps to identify the point at which the plot starts to become parallel to the x-axis. The K value corresponding to this point is the optimal number of clusters. In the below plot one is likely to select k=4. Currently the kmeans argument input only accepts Kmeans, MiniBatchKMeans, and BisectingKMeans.

plot.elbow_curve(X, kmeans, range_n_clusters=range(1, 30))

<Axes: title={'center': 'Elbow Plot'}, xlabel='Number of clusters', ylabel='Sum of Squared Errors'>

Tip

If you want to train the models yourself, you can use elbow_curve_from_results to plot.

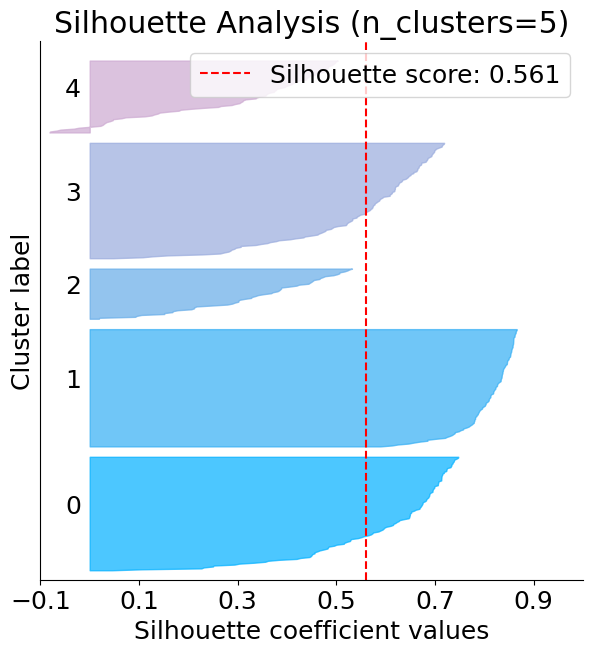
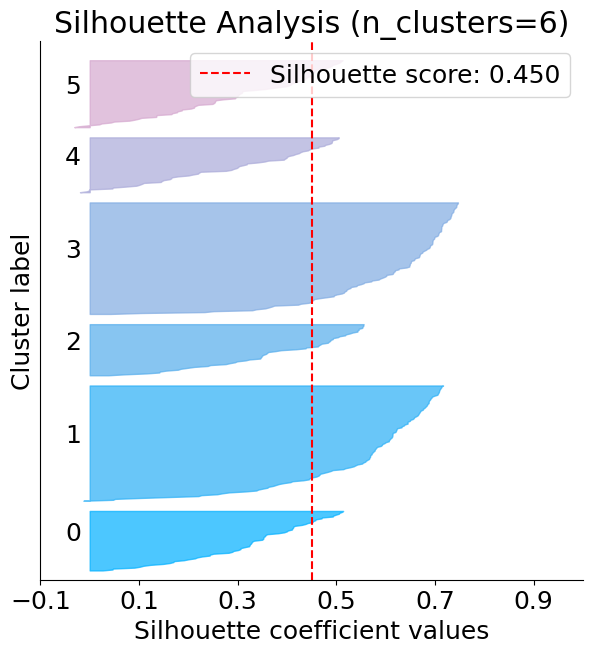
Silhouette plot

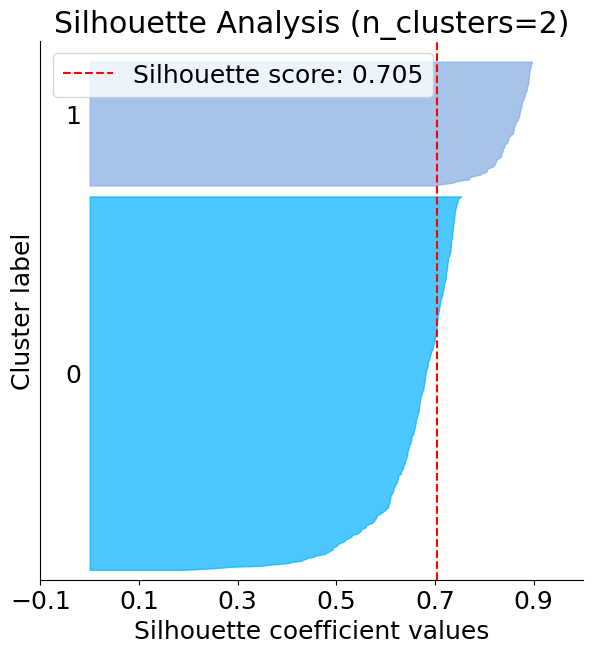
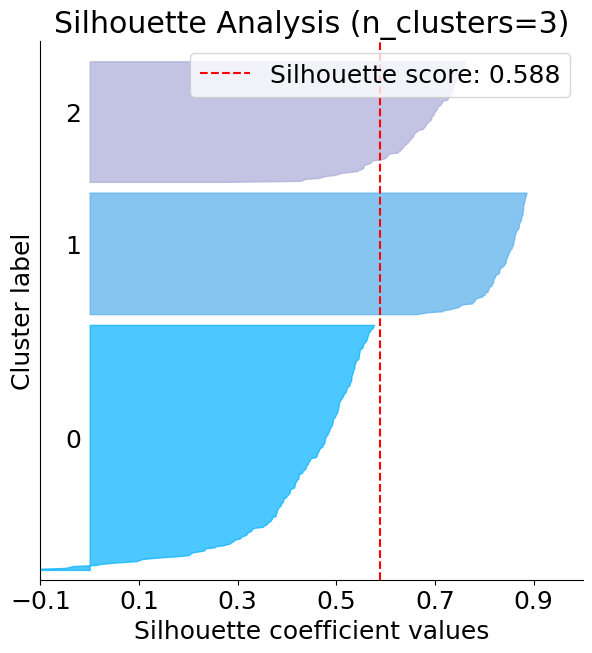
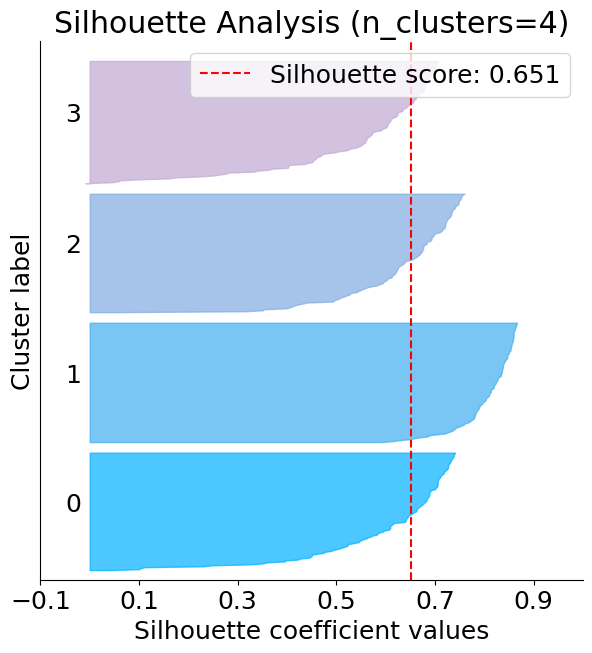
The below plot shows that n_clusters value of 3, 5 and 6 are a bad pick for the given data. One is likely to select between 2 and 4 n_clusters.

silhouette = plot.silhouette_analysis(X, kmeans)

Tip

If you want to train the models yourself, you can use silhouette_analysis_from_results to plot.